26 Sep 2019
Emmy Noether looks at the deconfined quantum critical point

Dr Ziyang Meng, HKU Department of Physics
A research team led by Dr Ziyang Meng from the Department of Physics has established an interesting connection between the classical Noether’s theorem in physics to the most modern quantum many-body research [1].
The German scientist Emmy Noether (1882 – 1935), perhaps the greatest female physicist and mathematician, has discovered an important theorem—Noether's theorem [2] —which relates symmetries with conservation laws. The theorem states that for every continuous symmetry generated by local actions, there corresponds a conservation law.
Applications of the theorem are everywhere in science, physics, chemistry, biology, such as the space-time translation symmetry gives rise to momentum-energy conservation, the rotation symmetry gives rise to angular momentum conservation, etc. However, over the years people turn to unconsciously relate the fundamental law of physics like Noether's theorem to classical and text-book examples, and rarely expect the immediate application of them in the frontier of research which is beyond any established paradigms.
In a recent research work [1], to one’s surprise, a team led by HKU physicist Dr Ziyang Meng establishes an interesting connection between the Noether’s theorem and the most modern quantum material research. In the work, Dr Ziyang Meng, Dr Nvsen Ma from the Institute of Physics, Chinese Academy of Sciences and Dr Yi-Zhuang You from University of California at San Diego, demonstrated an explicit application of the Noether's theorem in identifying the emergent continuous symmetry in an exotic quantum phase transition–the deconfined quantum critical point (DQCP), which is the quantum phase transition beyond the conventional paradigm of phases of matter. The work was published in the recent issue of Physical Review Letters. (link of the article).

Fig.1 Emmy Noether (1882 – 1935) was a German mathematician who made important contributions to abstract algebra and theoretical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed the theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws [2] (From Wikipedia). In the research work [1], a team lead by HKU physicist establishes an interesting connection between the Noether’s theorem and the most modern quantum material research.
In quantum many-body systems, the manifestation of symmetry can be much richer than that in their classical counterparts, new symmetry that does not exist in the microscopic model could emerge at low energy and lead to emergent conservation law. A great platform to test these ideas is the deconfined quantum critical point (DQCP). As schematically shown in Fig. 2, the DQCP is an exotic quantum critical point between two spontaneous symmetry breaking phases: the antiferromagnetic phase (AFM) and the valence bond solid (VBS) phase. Deconfined degrees of freedom, such as fractionalized spinons and emergent gauge fluctuations, appear at and only at DQCP. The fractionalization generally enlarges the scaling dimension of order parameters and makes other symmetry breaking terms irrelevant, which paves the way for larger symmetry to emerge.
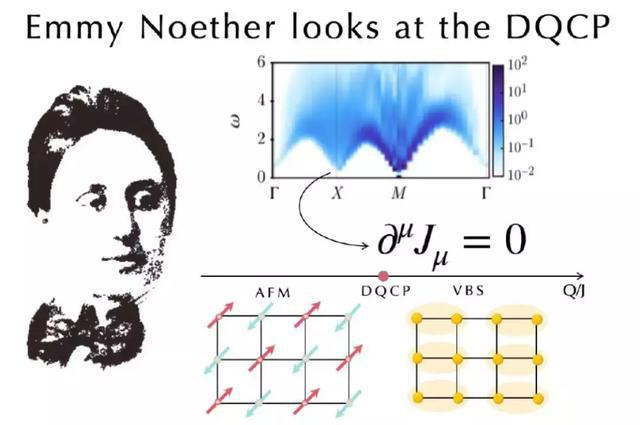
Fig.2. Schematic plot of the phase diagram of J-Q model with AFM and VBS phases and the deconfined quantum critical point (DQCP). At the DQCP, spin excitation at the momentum point X=(pi,0) is the conserved current of the emergent O(4) symmetry, therefore its scaling dimension is an integer value only related with space-time dimension of the model, and such conservation is identified from quantum Monte Carlo simulations in Ref. [1].
The research team investigated the two dimensional easy-plane JQ model as shown in Fig.2. According to the Noether’s theorem, every continuous symmetry of a physical system is associated with a corresponding conservation law, the conservation law further manifests itself in the form of a conserved current. Therefore, the observation of a conserved current in a physical system is the direct evidence of the existence of the associated continuous symmetry. At the DQCP shown in Fig. 2, the generators of emergent O(4) symmetry rotate between the AFM and VBS order parameters, the detection of its associated conserved current (the AFM-VBS current) would provide strong support for the emergent symmetry and hence the field theory description of the DQCP.
To test the proposition, the team performed large-scale quantum Monte Carlo simulations. They measured the dynamical spin correlation functions at the corresponding momenta, and found that its scaling dimension is indeed converged to the integer only related with the space-time dimension of the problem – the unique property of conserved current operator – precisely consistent with the requirement of the conservation law. Therefore the simulation results in Ref. [1] confirm the emergent O(4) symmetry at DQCP by measuring the associated emergent conserved current in the spin excitation spectrum.This study demonstrated an elegant yet practical approach to detect emergent symmetry by probing the spin excitation, which could potentially guide the ongoing experimental search for DQCP in quantum magnets. Moreover, the idea of employing conserved current to detect the emergent continuous symmetry in quantum many-body systems has also inspired several recent works [3,4,5]. It was expected that the research would further motivate active search and future experimental detection of quantum magnets that belong to the materials in new paradigms of quantum matter.
Acknowledgement
The large-scale simulations are performed on the Tianhe-1A platform at the National Supercomputer Center in Tianjin and Tianhe-2 platform at the National Supercomputer Center in Guangzhou, the authors acknowledge the technical support and generous allocation of CPU time from these centers. The authors also thank the funding support from the Ministry of Science and Technology of China through the National Key Research and Development Program (2016YFA0300502), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB28000000), the National Science Foundation of China (11574359,11674370) and the DFG research unit FOR1807 and Mercator Fellow.
The authors would like to thank the support from the “Computational Initiative – Towards Next-Generation Scientific Computing via Neuromorphic-AI Accelerators” at the Faculty of Science, the University of Hong Kong.
Journal Reference
[1] Role of Noether’s Theorem at the Deconfined Quantum Critical Point, Nvsen Ma, Yi-Zhuang You, and Zi Yang Meng, Phys. Rev. Lett. 122, 175701 (2019), https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.175701
[2] Noether, Emmy (1918), "Invariante Variationsprobleme", Nachr. D. Koenig. Gesellsch. D. Wiss. Zu Goettingen, Math-phys. Klasse, 1918: 235–257 Translated in Noether, Emmy (1971). "Invariant variation problems". Transport Theory and Statistical Physics. 1 (3): 186. arXiv:physics/0503066. doi:10.1080/00411457108231446
[3] Quantum phases of SrCu2(BO3)2 from high-pressure thermodynamics, Jing Guo, Guangyu Sun, Bowen Zhao, Ling Wang, Wenshan Hong, Vladimir A. Sidorov, Nvsen Ma, Qi Wu, Shiliang Li, Zi Yang Meng, Anders W. Sandvik, Liling Sun, arXiv:1904.09927
[4] Emergent Symmetry and Conserved Current at a One Dimensional Incarnation of Deconfined Quantum Critical Point, Rui-Zhen Huang, Da-Chuan Lu, Yi-Zhuang You, Zi Yang Meng, Tao Xiang
Phys. Rev. B 100, 125137 (2019) Editors' Suggestion
[5] Signatures of a Deconfined Phase Transition on the Shastry-Sutherland Lattice: Applications to Quantum Critical SrCu2(BO3)2, Jong Yeon Lee, Yi-Zhuang You, Subir Sachdev, Ashvin Vishwanath arXiv:1904.07266







