Introductioin
A collaboration between theoretical physicists Dr Chengkang ZHOU and Professor Zi Yang MENG from the Department of Physics at The University of Hong Kong (HKU), along with experimentalists Zhenyuan ZENG and Professor Shiliang LI at the Institute of Physics (IOP), Chinese Academy of Sciences (CAS), and Professor Kenji NAKAJIMA from J-PARC Center, Japan, has led to a discovery in the realm of quantum physics. Their study, published in a recent issue of Nature Physics, sheds light on the long-anticipated emergence of quasiparticles, akin to the famous Dirac particles obeying the relativistic Dirac equation. These quasiparticles, known as Dirac spinons, were theorised to exist within a novel quantum state called a quantum spin liquid state.
About the Research
Discovering the emergence of quasiparticles in condensed matter and quantum material analogous to the Dirac particles in high-energy physics has always been an interesting topic. These quasiparticles have a linear dispersion relation between the electronic energy and momentum. They are gapless fermions and can be handled theoretically by the relativistic Dirac equation. So far, Dirac fermions have been found in electronic systems like graphene and topological insulators. In quantum spin liquids – a novel quantum state expected to exist in frustrated magnets, theoretical predictions have suggested the existence of spinons, which are fractionalised quasiparticles carrying a spin of 1/2. In the gapless systems, the dispersion relation of these, named spinon excitations, can exhibit a form known as a Dirac cone (see the red cone Fig. 1a), giving rise to what is called a Dirac spinon. The existence of Dirac spinons has been highly anticipated in many theoretical models but the material realisation remains elusive due to the lack of spectra evidence. However, inelastic neutron scattering, one the most powerful and widely used tools for studying the spectra of spin excitations, has its limitations as it can only detect excitations involving two spinons. This means we cannot capture the signal from one spinon directly, but we can capture a pair of spinons with total spin-1 (see the blue cone in Fig. 1 a and b). Thus, although many quantum spin liquid candidates have been reported, none of them is consistent with the Dirac spinon excitations solidly.
Aiming to change this situation, a collaboration from theory (Dr Chengkang ZHOUand Professor Zi Yang MENG) from The University of Hong Kong) and experiment (Zhenyuan ZENG and Professor Shiliang LI at the Institute of Physics, Chinese Academy of Sciences and Professor Kenji NAKAJIMA from J-PARC Centre, Japan) made a discovery that has greatly changed the perplexing situation. They discovered the long-thought-after spin excitations with a conical spin continuum in a kagome lattice antiferromagnet. From this study, the theoretical and experimental physicists finally identified the novel quantum state of quantum spin with Dirac spinons.
The studied material is YCu3(OH)6Br2[Br0.33(OD)0.67] (denoted as YCu3-Br), where Cu2+ ions with spin of 1/2 form perfect kagome lattice. Previous studies (Phys. Rev. B 105, L121109 (2022) from the collaboration of Professor Meng and Professor Li) have shown that this spin system is highly likely to possess the ground state of a quantum spin liquid. Via the inelastic neutron scattering, the team now have discovered that the low-energy spin excitations in this system are located at six symmetric points in the Brillouin zone at low energies (Fig. 1b and 2a). As the energy increases, the excitations expand and eventually connect with each other (Figs. 2b-2d). The overall shape of the excitations resembles a cone (Fig. 2e), as depicted in Fig. 1b. Moreover, they found that the spin excitations are conical with a continuum inside. Further analysis shows a linear relationship between the half-width at half-maximum and the energy (Fig. 1c) is consistent with the characteristics of a Dirac cone.
Due to the limitations of the inelastic neutron scattering technique, we cannot directly detect the single spinon to unequivocally determine the nature of the emergent quasiparticles in this system. The spectral evidence arises from the comparison between the theoretical prediction, assuming that the emergent quasiparticles are magnons (linear spin waves) accompanied by two spinons, and the experimental results. Figure 3 (experimental result) and Figure 4 (theoretical prediction) clearly demonstrate distinct features. Notably, the real material exhibits a convolved cone structure with finite and continuous spectral weight inside the cone. In contrast, linear spin waves, even when considering the disordered effects on the spin coupling, do not possess any weight inside the cone and exhibit linearly dispersing magnons. These differences suggest that the spectral properties of the real material go beyond the framework of linear spin wave and instead correspond to the signal of spinons.
Finding spectral evidence of Dirac spinon excitations has always been a challenge. Their results provide strong evidence for the emergence of a Dirac quantum spin liquid state in our study, which can be likened to a loud baby crying amidst the investigation of spectral signatures related to Dirac spinon excitations. Our work captures the conic spin excitations arising from Dirac spinons, resulting in low-energy spin excitations with sharp energy-momentum characteristics. This makes YCu3-Br an intriguing platform for further experimental and theoretical studies.
This study entitled 'Spectral evidence for Dirac spinons in a kagome lattice antiferromagnet' was published on Nature Physics.
The study was supported by the Ministry of Science and Technology of China, the Chinese Academy of Sciences and grants from Hong Kong. Neutron scattering measurements were performed on AMATERAS, J-PARC.
Dr Chengkang Zhou and Professor Zi Yang Meng are supported by the Collaborative Research Fund (HKU C7037- 22GF) and ANR/RGC Joint Research Scheme (A_HKU703/22) of the Hong Kong Research Grants Council, highlighting the forward-looking perspective and support of the Hong Kong government in the research of quantum materials. The theoretical calculations conducted in this study were performed on the High-Performance Computing Platform HPC2021 at the Information Technology Services, HKU, and the ‘Blackbody’ supercomputer at the Department of Physics at HKU.
![Figure 1. a. Schematic diagram of the conical excitations of Dirac spinons and the conical continuum spectrum formed by two spinons. b. Schematic diagram of the conical spin excitations in YCu3(OH)6Br2[Br0.33(OD)0.67]. c. Relationship between the half-width at half-maximum and energy. The solid line represents a linear fit.](/f/page/8595/21173/500p311/image01.png)
Figure 1. a. Schematic diagram of the conical excitations of Dirac spinons and the conical continuum spectrum formed by two spinons. b. Schematic diagram of the conical spin excitations in YCu3(OH)6Br2[Br0.33(OD)0.67]. c. Relationship between the half-width at half-maximum and energy. The solid line represents a linear fit.
![Figure.2 Spin excitations in YCu3(OD)6[Br0.33(OD)0.67] measured via the neutron scattering. e,f, Intensity contour plots of the INS results as a function of E and Q along the [H, 0] direction at 0.3 K (e) and 30 K (f).](/f/page/8595/21173/500p532/image02.png)
Figure.2 Spin excitations in YCu3(OD)6[Br0.33(OD)0.67] measured via the neutron scattering. e,f, Intensity contour plots of the INS results as a function of E and Q along the [H, 0] direction at 0.3 K (e) and 30 K (f).
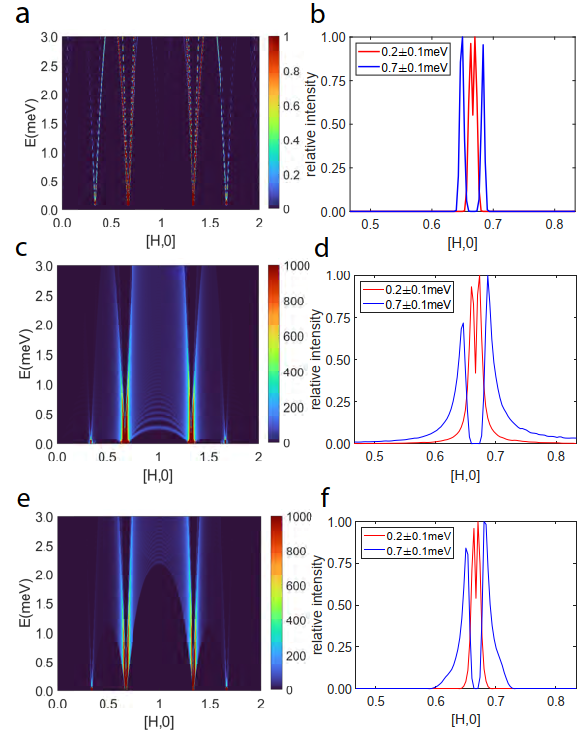
Figure.3 Linear spin wave prediction on the kagome lattice: a and b show the spin spectra without introducing disorder effects. c and d display the spectra with the same parameters but introducing disordered effects to fit the experimental results. e and f show the spectra with different kinds of disorder.

